Model Activity task 2021(July)
Class 9 Math( Part-4)
মডেল অ্যাক্টিভিটি টাস্ক ২০২১ |
নবম শ্রেণী গণিত( পার্ট -৪)
নীচের প্রশ্নগুলির উত্তর লেখো :
1.বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs) :
(i) π একটি
(a) মূলদ সংখ্যা
(b) পূর্ণ সংখ্যা
(c) বীজীয় অমূলদ সংখ্যা
(d) তুরীয় অমূলদ সংখ্যা
(ii) 0 –এর n তম মূল
(a) 1 (b) 0 (c) একটি অমূলদ সংখ্যা (d) এর অস্তিত্ব নেই
(iii) y +7= 0 সমীকরণটির লেখচিত্রটি
(a) y-অক্ষের সমান্তরাল
(b) x-অক্ষের সমান্তরাল
(c) y-অক্ষের সঙ্গে 0° কোণ করে
(d) x-অক্ষের সঙ্গে 90° কোণ করে
(iv) x + y = 20, 10x+5y = 140 সহসমীকরণের
(a) একটি মাত্র নির্দিষ্ট সাধারণ সমাধান থাকবে
(b) দুটি নির্দিষ্ট সাধারণ সমাধান থাকবে
(c) অসংখ্য সাধারণ সমাধান থাকবে
(d) কোনো সাধারণ সমাধান থাকবে না ।
- সত্য / মিথ্যা লেখো (T/F) :
(i) কোনো চতুর্ভূজাকার ক্ষেত্রের একটি কর্ণ চতুর্ভুজাকার ক্ষেত্রের বাইরে থাকলে, চতুর্ভূজাকার ক্ষেত্রের চতুর্ভুজটি একটি সামান্তরিক।
মিথ্যা
(ii) রম্বসের একটি কোণ সমকোণ হলে রম্বসটি একটি বর্গক্ষেত্র।
সত্য
(iii) বহুপদী সংখ্যামালায় চলের সূচক যে কোনো পূর্ণসংখ্যা হবে।
মিথ্যা
(iv) 0 একটি ধ্রুবক বহুপদী সংখ্যামালা এবং শূন্য বহুপদী সংখ্যামালাও।
সত্য
- সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) g(x) =2x-16 বহুপদী সংখ্যামালাটির সমীকরণটি লেখো এবং বহুপদী সংখ্যামালাটির শূন্য নির্ণয় করো।
সমাধানঃ g(x) =2x-16 বহুপদী সংখ্যামালাটির সমীকরণ নির্ণয়ের শর্ত
g(x)= 0
∴2x-16=0
∴g(x) বহুপদী সংখ্যামালাটির সমীকরণটি হল
2x-16=0
বা, 2x = 16
বা, x = 8
X= 8 এর জন্য g(x) এর মান 0 হবে
অতএব , g(x) বহুপদী সংখ্যামালাটির শূন্য হলো 8
(ii) (8x3 + 8x- 5) বহুপদী সংখ্যামালাটির একটি উৎপাদক নির্ণয় করো।
সমাধানঃ 8×3+8x−5
= 8x3−1+8x−4
= (2x)3−(1)3+8x−4
= (2x−1){(2x)2+2x.1+(1)2}+4(2x−1)
= (2x−1)(4x2+2x+1)+4(2x−1)
= (2x−1)(4x2+2x+1+4)
= (2x−1)(4x2+2x+5)
উত্তরঃ 8x3 + 8x- 5 বহুপদী সংখ্যামালাটির একটি উৎপাদক হলো (2x-1) ।
(iii) (−2, −2) এবং (4, 6) বিন্দু দুটির মধ্যে দূরত্ব নির্ণয় করো।
সমাধানঃ ধরি P (−2, −2) ও Q(4,6) বিন্দু দুটির মধ্যে দূরত্ব নির্ণয় করব ।
বিন্দু দুটির মধ্যে দূরত্ব (PQ) = √(x1−x2)2+(y1−y2)2
=√(−2−4)2+(−2−6)2 একক
= √(−6)2+(−8)2 একক
= √36+64 একক
=√100 একক
= 10 একক
উত্তরঃ (−2, −2) এবং (4, 6) বিন্দু দুটির মধ্যে দূরত্ব 10 একক ।
- যুক্তি দিয়ে প্রমাণ করো, যে কোনো চতুর্ভুজের একজোড়া বিপরীতবাহু সমান ও সমান্তরাল হলে, চতুর্ভুজটি সামান্তরিক হবে।
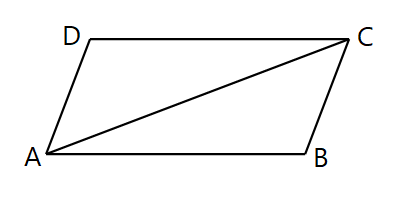
প্রদত্তঃ ABCD একটি চতুর্ভুজ যার, AB=DC এবং AB∥DC
প্রামাণ্য বিষয়ঃ ABCD একটি সামান্তরিক ।
অঙ্কনঃ A ও C যুক্ত করে AC কর্ণ আঁকলাম ।
প্রমানঃ △ABC ও △CDA এর –
AB=DC (প্রশ্নে বলা আছে )
∠BAC=∠BAC= একান্তর ∠ACD∠ACD [∵AB∥DC এবং AC ছেদক ও ওদের সাধারণ বাহু। ]
∴ △ABC≅△CDA [ S-A-S সর্বসমতার সূত্র অনুযায়ী ]
সুতরাং ∠ACB=∠DAC [সর্বসম ত্রিভুজের অনুরূপ কোণ ]
কিন্তু BC ও AD সরলরেখাংশকে AC ছেদ করেছে । তাই দুটি একান্তর কোণের মান সমান।
∴ BC∥AD
যেহেতু, ABCD চতুর্ভুজের AB∥DC ও BC∥AD তাই প্রমাণিত হল যে ,
ABCD একটি সামান্তরিক (প্রমাণিত)।
Click Here To Download The Pdf



