Model Activity task 2021(July) Class 10 Math ( Part-4) মডেল অ্যাক্টিভিটি টাস্ক ২০২১ | দশম শ্রেণী গণিত( পার্ট -৪)

Model Activity task 2021(July)

Class 10 Math ( Part-4)

মডেল অ্যাক্টিভিটি টাস্ক ২০২১ |

দশম শ্রেণী গণিত( পার্ট -৪)

নিচের প্রশ্নগুলির উত্তর লেখ :

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQ)

(i) বাস্তব সহগ যুক্ত একচলবিশিষ্ট দ্বিঘাত সমীকরণটি হল

(a) x(x²−1)−3x=0 (b)  x²(x²−1)−6x=0 (c)  x(x-1)-x=0  (d) 2x−4=0

(ii) (2x-2)(x+3)=0 সমীকরণটির বীজ দুটি হলো

(a)   -1,-3  (b)  -1,3  (c)  1,-3  (d) 1,3

 (iii) বার্ষিক 10% সরল সুদের হারে 50 টাকার 2 বছরের সুদ ঐ একই হারে 100 টাকার 1 বছরের সুদের

(a) দ্বিগুণ (b) অর্ধেক (c)  এক চতুর্থাংশ  (d) সমান

(iv) O কেন্দ্রীয় বৃত্তের PQ ও RS দুটি সমান দৈর্ঘ্যের জ্যা । O বিন্দু থেকে PQ জ্যা এর দূরত্ব 8 সেমি. হলে , O বিন্দু থেকে RS জ্যা এর দূরত্ব কত?

(a)8 সেমি   (b)16 সেমি (c)4 সেমি    (d)10 সেমি

∠OCQ=ODS=90º

OQ=OS

CQ=DS

∴  △COQ ও △ODS পরস্পর সর্বসম।

∴  OC=OD=8 সেমি ।

2. সত্য / মিথ্যা লেখ (T/F)

(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য অর্ধেক করা হলে , ঘনকটির আয়তন প্রথম আয়তনের  1/8 অংশ হবে।

সত্য (T) ।

সমাধানঃ

ধরি ঘনকটির প্রাথমিক বাহুর দৈর্ঘ্য ছিল 2a । অর্থাৎ অন্তিম দৈর্ঘ্য ছিল a ।

আমরা জানি , ঘনকের আয়তন = (বাহু)³

অতএব, প্রাথমিক আয়তন= (2a)³ = 8a³

এবং , অন্তিম আয়তন =(a)³ = a³

এখন,( অন্তিম আয়তন ÷ প্রাথমিক  আয়তন) =a³ / 8a³= 1/8

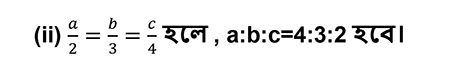
 (iv) চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস । বৃত্তের ভেতরে Q একটি বিন্দু । ∠AQB সর্বদা সূক্ষ্মকোণ ।

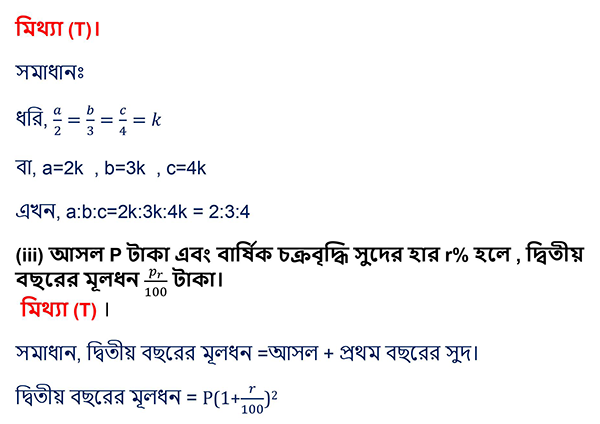
মিথ্যা (T) ।

3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

i)একটি লম্ববৃত্তাকার চোঙের আয়তন ও বক্রতলের ক্ষেত্রফল সাংখ্যমানে সমান হলে, উহার ব্যাসার্ধ নির্ণয় করো

বা, r=2

উঃ লম্ববৃত্তাকার চোঙের ব্যাসার্ধ 2 একক।

4.যুক্তি দিয়ে প্রমাণ করো যে, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পুরক ।

Click Here To Download The Pdf